포스팅 목적

- heapify 이해하기

- siftup , siftdown 이해하기

- build Heap Time Complexity : O(n) 이해하기

 

 

 

Heap 을 구성하는데 O(n)의 시간복잡도를 갖음을 이해하는데 앞서 가장 간단한 방법을 생각해봅시다.

 

힙 아키텍쳐에 임의의 순서로 나열된 n개의 데이터 셋을 저장하기 위해서

우리는 데이터 셋을 순차적으로 힙에 삽입하는 방법을 생각할 수 있을 것입니다.

 

1. 힙에 순차적인 데이터 삽입 시간복잡도  : O(nlogn)

 

결론적으로 n 개의 데이터를 힙 자료구조에 순차적으로 삽입할 경우 O(nlogn) 시간복잡도를 갖습니다. 

 

직관적으로 볼때 힙의 삽입은 O(logn) 의 시간복잡도를 갖고 , n 개의 데이터를 순회하며 삽입하기 때문에

총 시간복잡도는 O(nlogn)를 갖는다고 여길 수 있지만, 이는 옳바른 접근이 아닙니다.

 

힙의 시간복잡도 n은 힙을 구성하는 size를 의미하기 때문에 n개의 데이터를 순차적으로 삽입함에 따라

힙을 구성하는 n은 1~n 까지 순차적으로 증가해야 합니다.

 

결론적으로 O(log1 +log2 + log3 + ....  + logn) 의 시간복잡도를 갖게될 것 입니다.

 

이는 Stirling's approximation 에 의해 O(nlogn)로 계산됩니다.

 

 

 

 

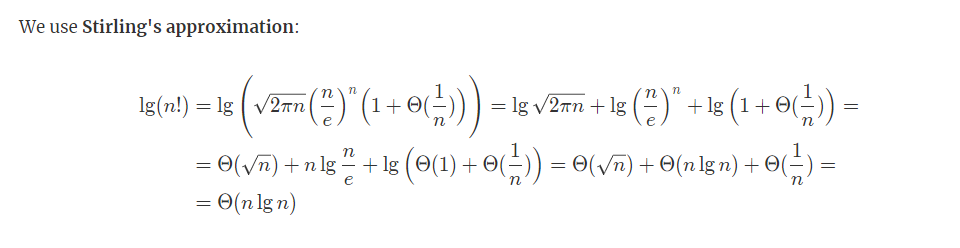
2. Heapify(Sift Down) 를 이용한 시간복잡도 : O(n) 

 

임의의 n개 데이터를 heap 아키텍쳐로 바꾸는 과정은 2가지로 접근할 수 있습니다.

1. Sift Up Operation

2. Sift Down Operation 

 

해당 글을 이해하기 전에 용어를 살펴봅시다. 

 

- Sift up

Sift up은 heap에 데이터를 삽입하는 과정에서 발견할 수 있습니다.

 

heap에 데이터를 삽입하는 경우, 삽입된 데이터는 최초로 완전이진트리의 leaf 부분에 위치할 것 이며,

이후, 삽입 노드의 부모 노드 값과 비교연산을 수행하며 Swap이 발생할 것 입니다.

 

위에서 발견할 수 있듯이 Sift Up 은

주어진 노드의 부모 노드와의 비교연산을 수행하여 이를 만족시키거나, 그렇지 않으면 root에 도착할 때 까지 Swap하는 방법을 의미합니다.

 

 

 

- Sift down

 

반대로 Sift down은 heap에서 데이터를 삭제하는 과정에서 발견할 수 있습니다.

 

heap에서 데이터를 삭제하는 경우, 완전이진트리(힙)의 leaf 노드를 root로 이동시켜 child's의 노드와 비교연산을 수행하여, heap property를 만족하지 않으면 swap할 것 입니다.

 

Sift Down은 

주어진 노드의 child node's 중 key가 큰 값(or 작은 값) 과 비교연산을 수행해 property를 만족하거나, 그렇지 않으면 leaf에 도착할 때 까지 swap 하는 과정을 의미합니다.

 

 

 

 

1. Sift Up 을 이용한 build heap 예시

 

이 방법은 힙에 순차적으로 데이터를 삽입하는 방법과 거의 유사합니다.

(sift up operation은 힙에 데이터 삽입에서 발생하기 때문)

 

예시를 통해 이해해 보겠습니다. (max heap을 가정)

위와 같은 무작위의 데이터 set 이 있을때, 앞에서부터 순차적으로 접근합니다.

(1)

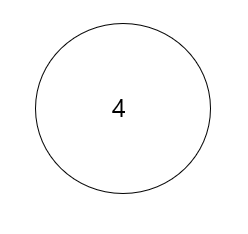
처음 data 4는 sift up의 definition에 따라 부모 노드와 값을 비교해야 합니다. 해당 부모 노드가 존재하지 않으므로 연산은 종료됩니다.

 

(2)

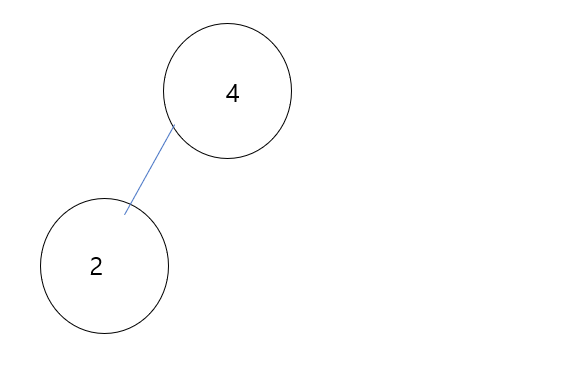
이후 삽입된 2는 sift up 연산에 의해 부모 노드와 비교가 일어나고 주어진 비교연산을 만족하므로 swap이 일어나지 않습니다.

 

(3)

삽입된 6 node의 데이터와 부모 노드간 비교연산을 수행합니다. heap property를 만족시키기 위해 swap이 발생합니다.

이후 swap된 6 은 root 에 존재하므로 재귀적인 연산을 종료합니다.

 

(4)

삽입된 8 과 부모 노드 2 간 비교연산을 수행합니다. 여기서 heap property를 만족하기 위해 swap이 발생합니다.

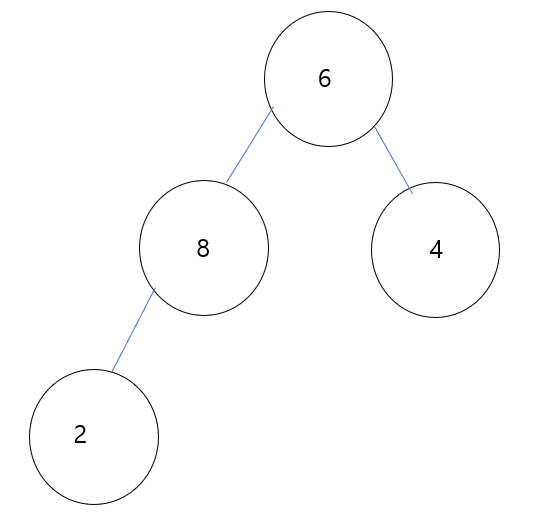
위에 정의했듯이 sift up 연산은 비교연산을 만족하거나, root에 존재할 때 까지 swap이 발생합니다.

(그렇기에 시간복잡도는 O(logn)) 

 

8 은 부모노드 6과 비교연산을 수행하며 이는 max heap property를 만족시키지 않으므로 또 한번의 swap이 발생할 것 입니다.

8은 root 에 존재하게 되므로 sift up 연산을 종료합니다.

 

 

 

2. Sift Down 을 이용한 build heap 예시

 

sift down은 위와 같은 방향으로 수행될 수 있습니다. 

 

(1) 우선 주어진 data set에 대응하는 완전 이진트리를 먼저 그리겠습니다.

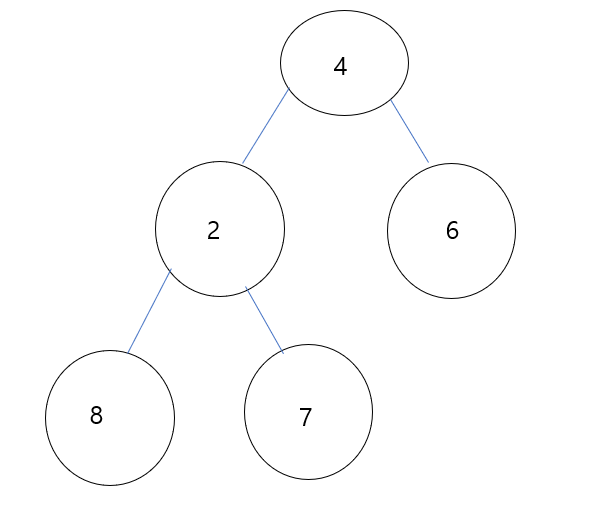
(2) 위에서 정의한 정의를 떠올려봅시다.

 

 

역방향으로 순차적으로 순회할 때 7,8,6 데이터는 leaf 에 존재하므로 swap을 수행하지 않습니다.

 

(3)

2의 경우 sift down에 의해 child node 중 큰 값 8과 비교 연산을 수행하고 swap이 발생합니다.

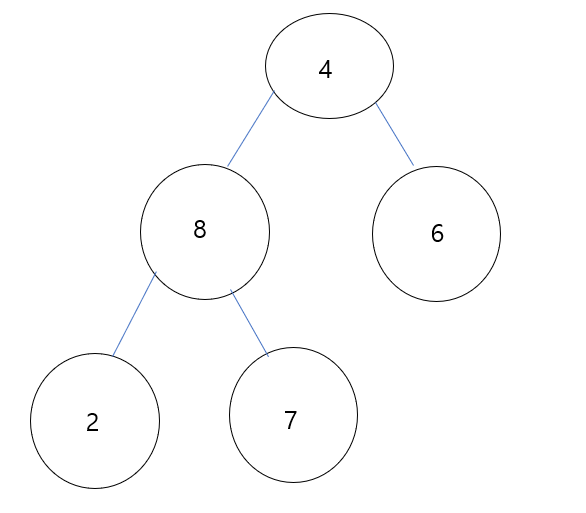
swap 발생 이후, 2는 leaf에 존재하므로 재귀적인 sift down 연산을 종료합니다.

 

(4) 

마지막으로 4 node는 child 중 값이 큰 8 데이터와 비교 연산을 수행하며 swap이 발생합니다.

이후, 4 데이터는 재귀적으로 다시 child node 중 큰 데이터와 비교연산을 수행하고, swap이 발생합니다.

4는 leaf에 존재하므로 sift down 연산을 종료합니다.

 

 

 

 

Build Heap 직관 및 결론

결론적으로 말하면 build Heap을 Sift Up 을 통해 구성하면 O(nlogn)의 시간복잡도를 갖으며, 

Sift Down 을 통해 구성하면 O(n)의 시간복잡도를 갖습니다.

 

수학적 수식을 보기전에 이를 직관으로 이해해 봅시다. 

 

Sift Up과 Sift Down은 둘 다 O(logn)의 시간 복잡도를 갖습니다. 하지만 그 과정을 좀 더 면밀히 살펴보면

 

Sift Up의 시간복잡도는 주어진 노드부터 root Node 까지의 높이 로 볼 수 있으며

Sift Down의 시간복잡도는 해당 노드부터 leaf Node 까지의 높이입니다. 

 

힙을 구성하는 완전이진트리는 그 성질에 의해 약 n/2 개의 노드는 leaf 노드에 존재하게 됩니다.

그러므로, Sift Down Operation으로 Heap을 설계하는 것이 더욱 효율적일 것임을 추론할 수 있습니다.

 

Sift Down의 Build Heap Time Complexity
Sift Up 연산 Build Heap 시간복잡도

Sift Down Time Complexity proof

 

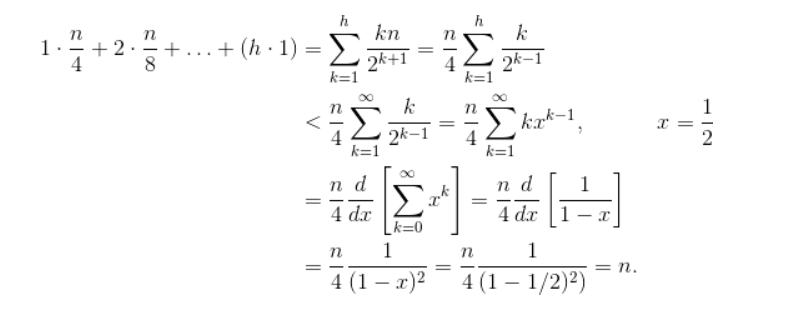
해당 Sift Down의 시간복잡도는 Taylor 급수를 기반으로 증명될 수 있으며 O(n) 의 시간복잡도를 갖습니다.

 

 

heap STL의 시간복잡도를 살펴보면 O(n)의 시간복잡도를 갖음을 확인할 수 있으며, 내부적으로 Sift Down으로 구현됨을 추정할 수 있습니다.

 

저작자표시

+ Recent posts

티스토리툴바